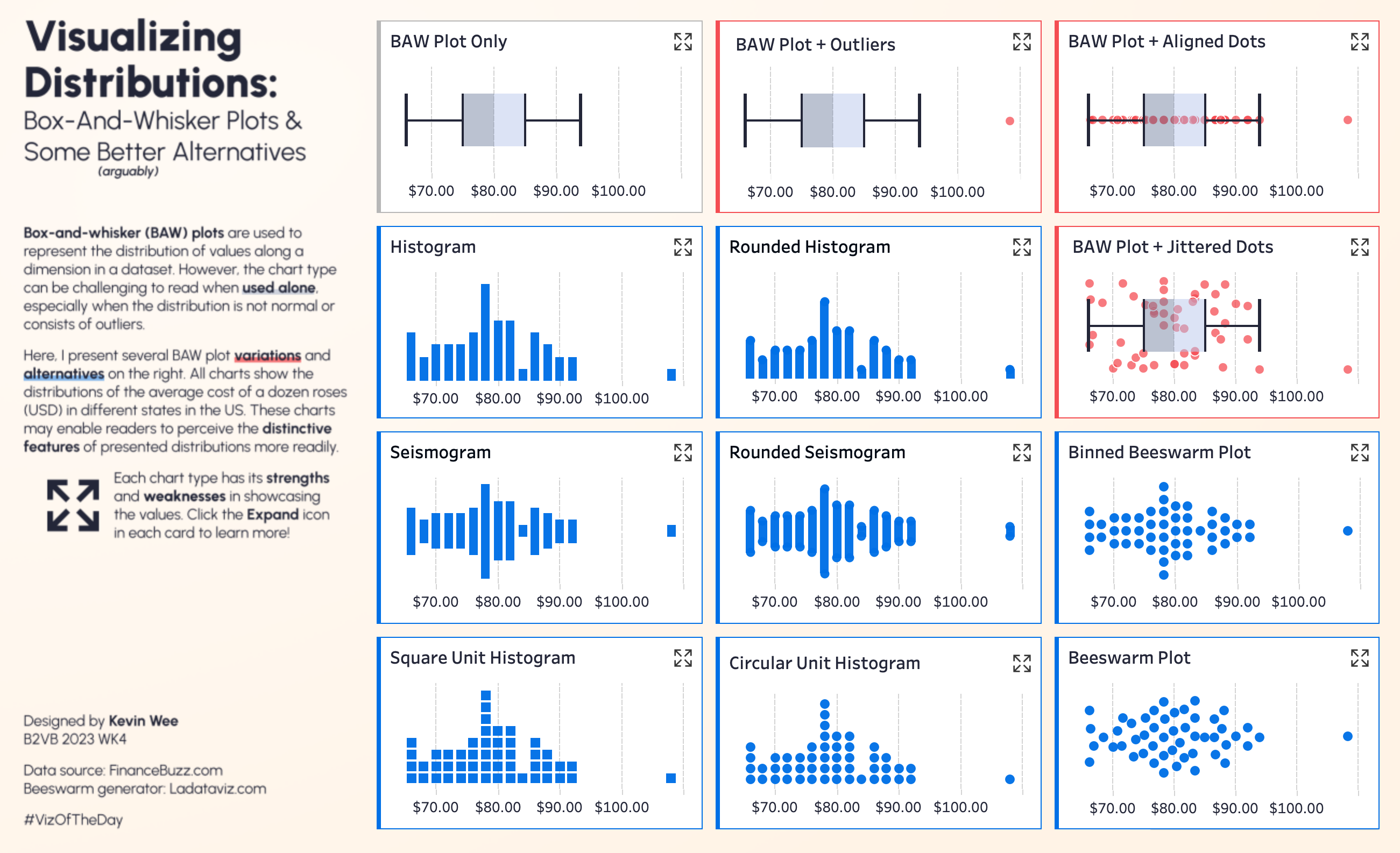
在日常分析中，分布可视化是最能体现数据细节和特征的手段之一。比如，许多人习惯用箱线图来展示一组数据的中位数、四分位数、异常值等信息。但仅仅依靠箱线图，真的能看懂数据分布里的所有细节吗？

出于对此问题的思考以及受到“数据可视化辞典”的启发，数据粉 Kevin Wee 基于一组美国各州玫瑰花价格的数据，梳理出一个关于“箱线图及其更优替代方案”的 Viz，并逐一剖析每种方案的优势与适用场景。

今天，让我们一起探索 Viz，看看如何助你选出更适合分析需求的数据分布图表吧！

01 标准箱线图

作为可能最早接触到的分布可视化方式之一，箱线图通过一个“箱子”和两根“须”，助你快速了解数据的分布大致情况：数据主要集中在哪里，整体的范围有多宽。

如下图所示，这是一款非常经典的“箱线图”：

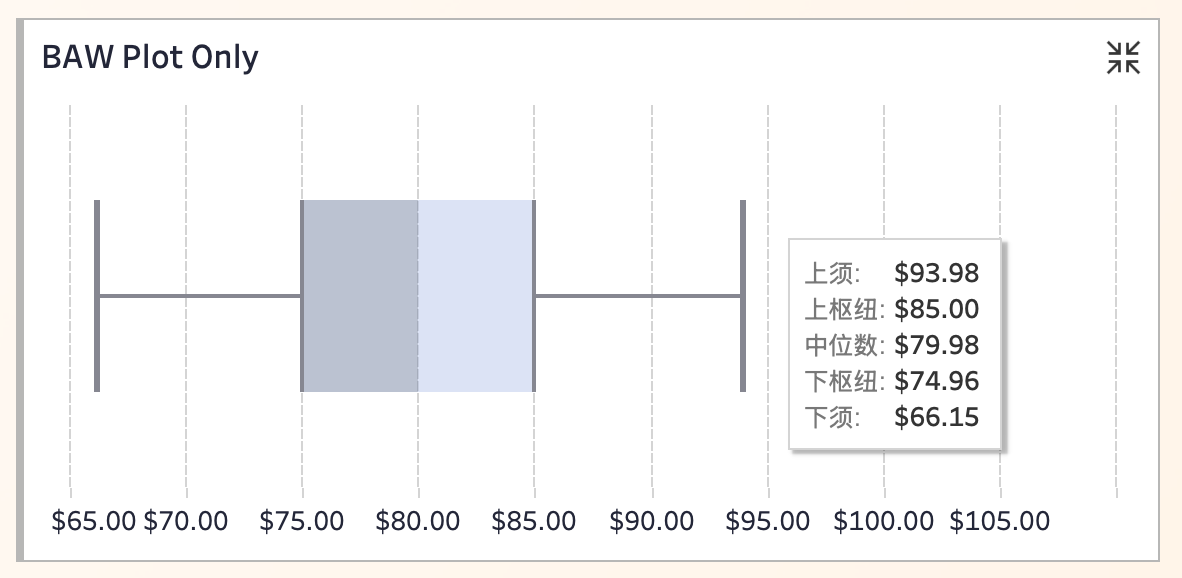
• 箱体的两端分别对应数据的四分位数；中间线代表中位数。即中间箱体部分覆盖了数据的中位数及上下四分位。

• 两边的“须”会延伸到数据分布的上下界线，表示数据分布在 1.5 倍四分位距以内的范围。但遇到极端值（异常值）时，通常会被忽略不显示。

结合数据来看，箱体横跨 $74.96 到 $85.00 ，说明有一半以上的价格都集中在这个区间。中间线（$79.98）代表着整个分布的中位数，也就是数据的“腰线”。下须和上须则分别标示了数据在四分位数之外的分布范围，提供了玫瑰花价格的整体波动概览。

换句话说，美国各州玫瑰花的主流价格集中在 75 美元到 85 美元之间，极端价格也没有特别离谱的异常点，整体分布较为对称。

不过， Kevin 不推荐单独使用这种方式来展示数据分布，建议配合其他分布型图表一起看：

👉 优点：箱线图非常适合对比多组数据，或快速了解一组数据的分布宽度和中位趋势。

👉 局限：如果你想深入了解每个数据点的分布细节，或数据本身偏斜、异常值较多，这个图就有点力不从心了。另外，不同工具对“须”的定义可能不一样，也可能影响解读。

02 箱线图 + 异常值

相比标准箱线图，这种做法在展示常规分布的同时，也把超出正常区间的数据点（异常值）直接用红色圆点标记出来，让极端值一目了然。

结合数据看，大多数州的玫瑰花价格集中在 75-85 美元之间。而右侧出现的红色异常点，表示远高于常规范围的价格。通过工具提示，可以发现这个异常点来自夏威夷（Hawaii），价格明显比其他州高出一大截，是典型的离群点。

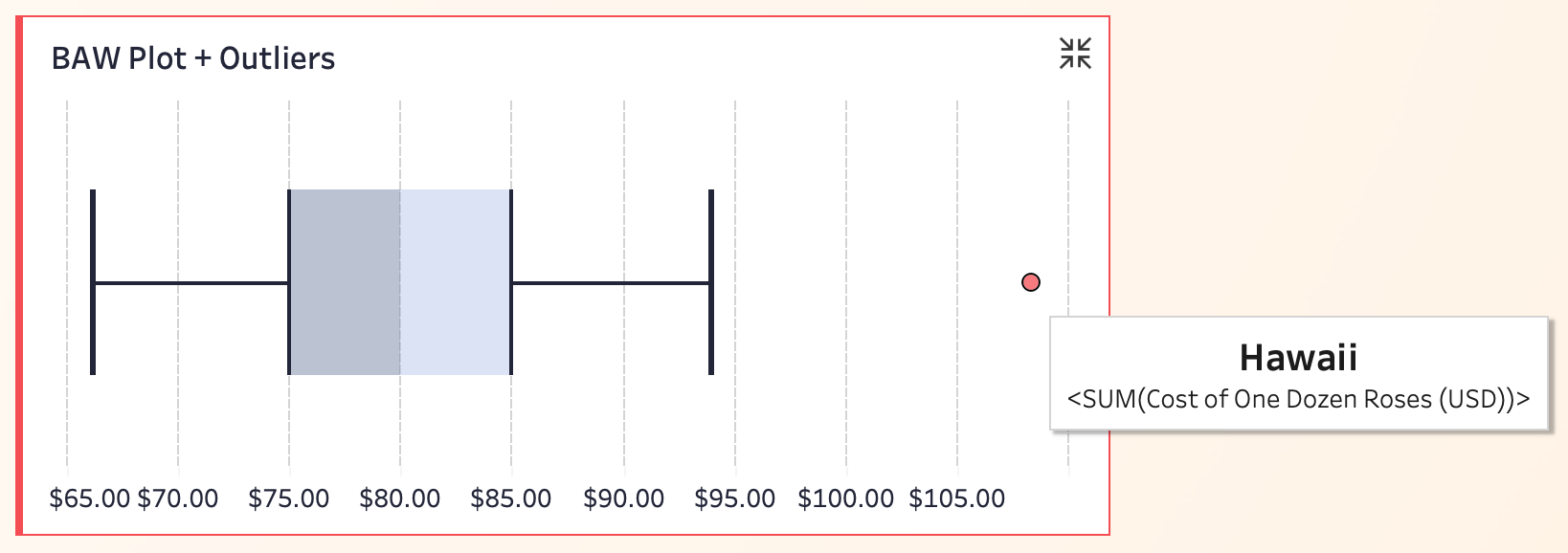
👉 优点：能让你一眼捕捉到数据分布的大致区间，并立刻识别出远离主流的数据点。例如，如果只看箱线图，夏威夷的价格就会被“隐藏”，但加上异常点标注后，就能轻松发现。

👉 局限：虽然异常值更醒目，但箱线图对主流分布内部的细节依然不够敏感，比如局部高密度的价格分布或者多个“扎堆”区间，还是无法直接展示。

03 箱线图 + 对齐点

相比前 2 个方案，这种方式更加“开门见山”。每个州的价格点排列在中线上，既能看分布趋势，也不会遗漏实际值。

如图所示，可通过工具提示查看每个州的玫瑰花售价。例如，康涅狄格州（Connecticut）的花价大约在 $90.00。正好在“上须”附近，属于价格相对较高但又没有达到异常值的那一批。

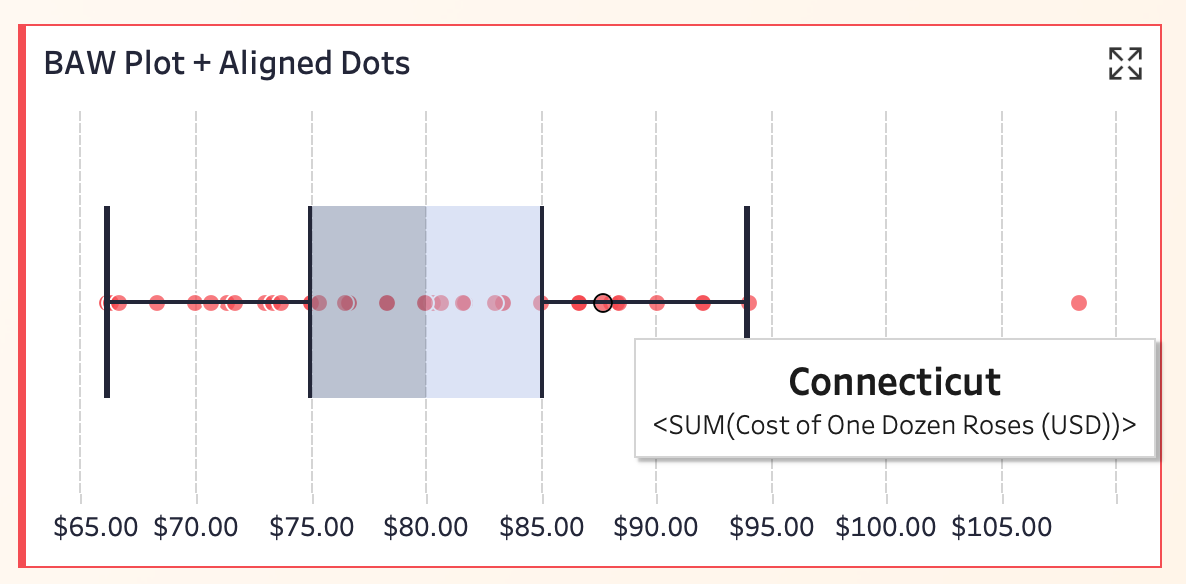
👉 这类图表既继承了之前的所有优点，又极大提升了“查个体、看分布”的能力，既能服务全局，又能关注细节，是分布类可视化里很实用的进化型方案。

👉 但也具有一些缺点：

• 数据量大时，圆点可能重叠太多，不易分辨具体数量

• 局部密集分布时，有些点会被箱体遮挡

• “须”的定义依然有不同解释，阅读时需注意

如需实现类似效果，可参考：举个栗子！Tableau 技巧：用「小提琴图 Violin Plot」 呈现盒须图的数据密集度。

04 直方图

在经历了各种进化版箱线图后，直方图（Histogram）带来了更直观、更细腻的分布可视化方式。

如果说前面的箱线图更强调区间划分与异常值定位，那么直方图就直接展示了每个价格区间内的观测值数量，让分布结构变得一目了然。

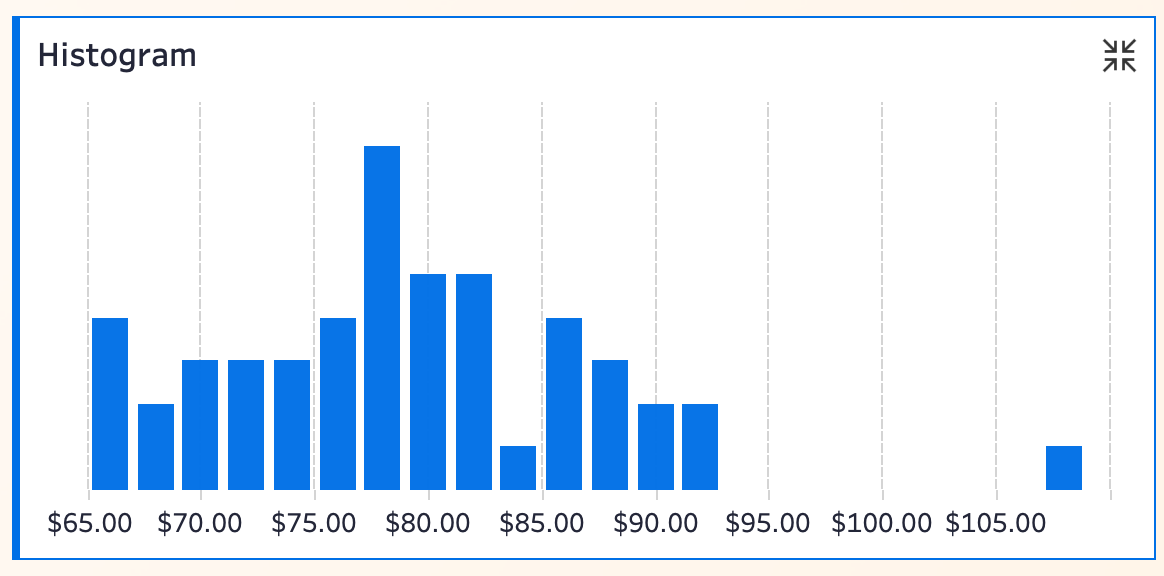
结合数据来看，$78.00-$79.99 这一档有 8 个州，是数据最密集的区间。相比只能看到“箱体宽度”的箱线图，直方图能精确量化“哪个价格段有多少州”。而在 $105 之后的区间，只出现了 1 个州，这样的突出异常点在直方图中同样不会被遗漏。

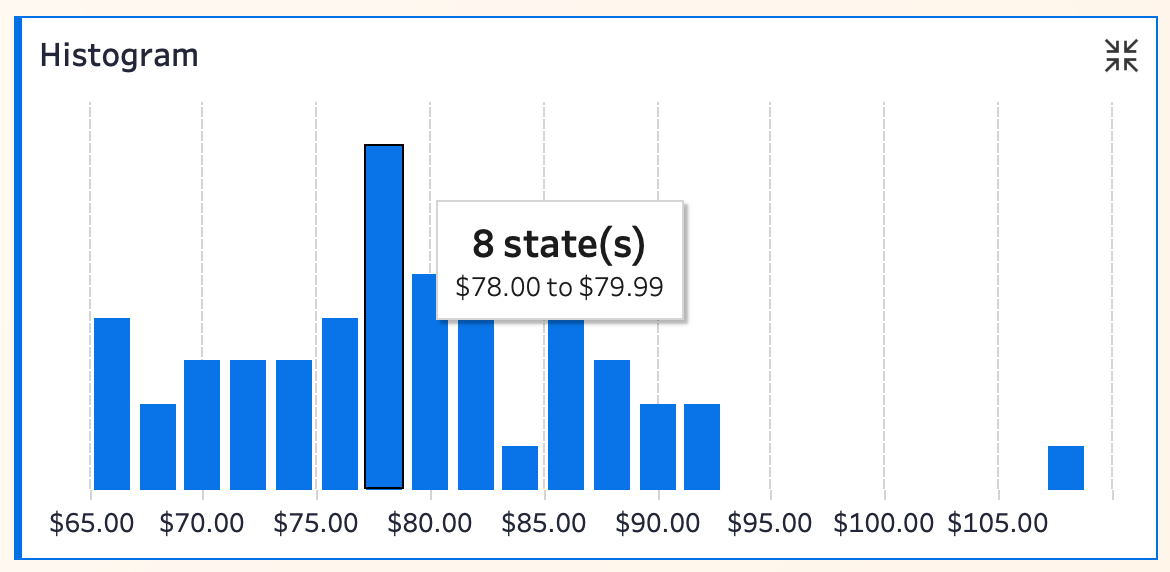
👉 Kevin 认为，直方图的优势在于各个价格段的“高峰”与“低谷”一览无遗，极其适合样本量较大、数据分布不均匀的场景。并且，“数据桶”的概念非常直观，易于理解和讲解。此外，虽然异常值不如箱线图那么“显眼”，但在极端区间依然能一眼发现。

👉 不足的是，直方图的分布形态会受到数据桶宽度的影响，宽了会遮住细节，窄了可能显得杂乱。其次，Tableau 的自动分桶有时不够“智能”，需要手动调整，才能展现出理想效果。

05 圆角直方图

相比上一版“标准直方图”，这一方案只是把原本方正的柱体换成了圆角，对视觉美观性进行了小幅升级。

除了数据结构与分布结论方面与直方图一致，圆角直方图最大的变化在于“看起来更舒服”，但美观性提升未必值得额外的制作精力投入，因此在注重展示美学或客户体验时可以优先选用。

06 箱线图 + 抖动点

在“箱线图+对齐点”的基础上，这一方案通过“抖动”让每个数据点在竖直方向随机散开，避免所有点都重叠在一条线上。

这样，报表用户不仅能看到每个观测值，还能直观感受到数据分布密度。同时也可发现，在分布密度大的区间里，抖动点会更多、更集中、更一目了然。

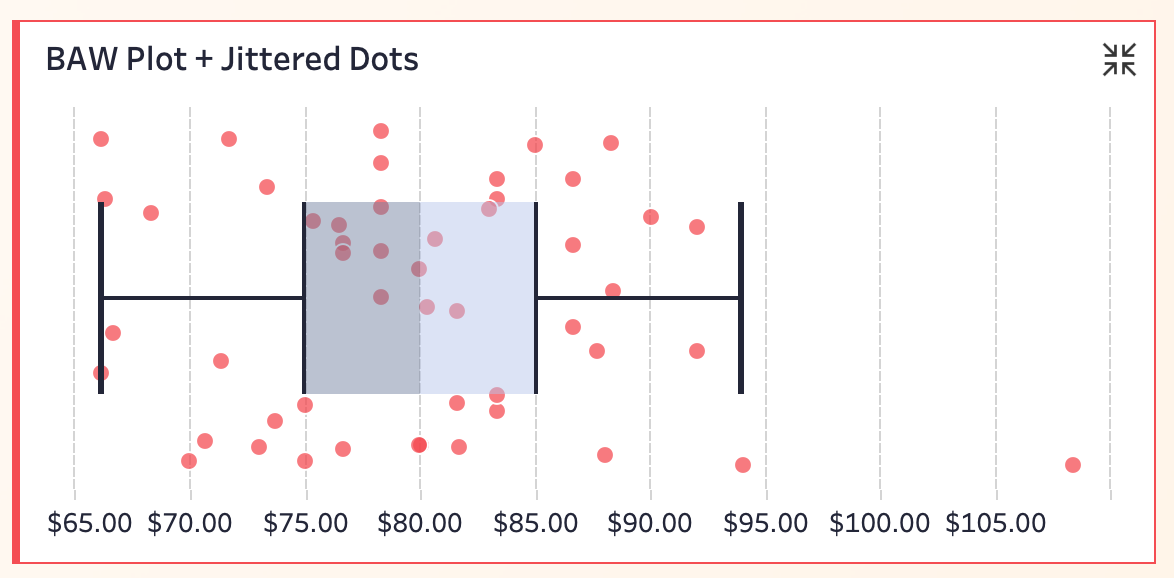
结合数据来看，绝大部分价格点还是集中在 $75-$85 这个区间，夏威夷的极高售价（异常值）依然很突出。

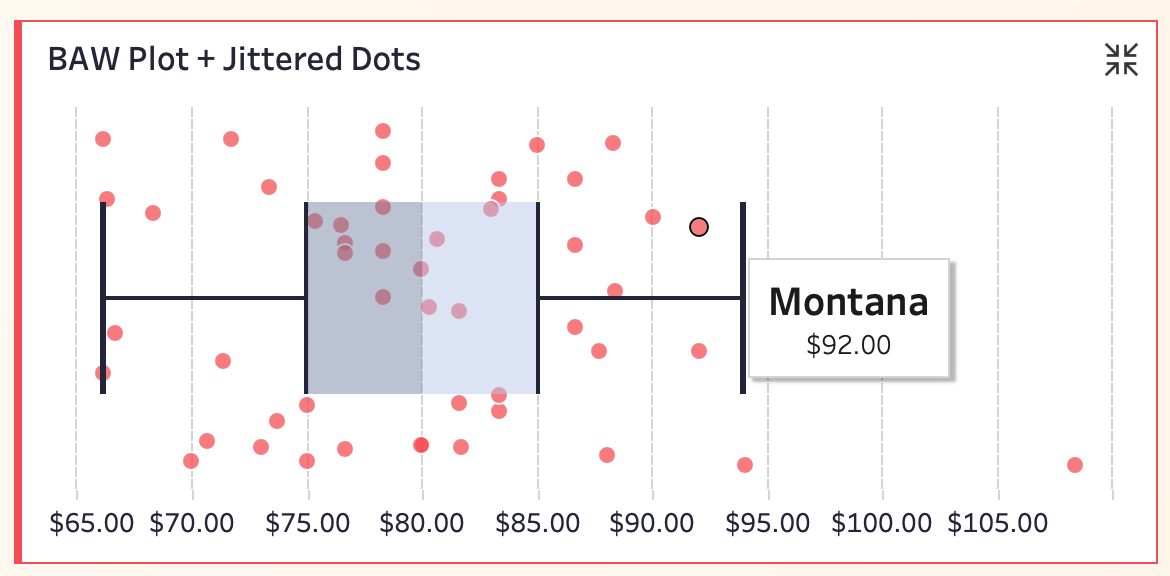
👉 Kevin 认为，这一方案很好解决了点重叠的问题，细节丰富，异常值突出。

👉 对于初学者来说，竖直方向的随机散开，有时容易让人误读为“Y 轴有意义”。实际上 Y 轴仅作区分，不能用于解读。此外，当数据量进一步增大时，仍然会出现点遮挡，尤其在主流区间。而且，抖动点太多也可能让人误以为是散点图而不是分布图。

如需实现类似效果，可参考：举个栗子！Tableau 技巧：用「抖动散点图 Jitter plot」呈现盒须图数据分布

07 震波图

你可以把震波图理解为“镜像版直方图”，它将直方图在中轴线上垂直对称展开，让分布特征看起来像地震或声音波纹，不仅增强了分布的层次感，也让高峰和低谷更加一目了然。

结合数据来看：波峰明显的区间（柱子长，比如 $80 前后）依旧是主力价格段；波谷（柱子短甚至消失，比如 $85-$87 的定价）较为稀少。异常点（$105 以上）依然以“孤岛”凸显。

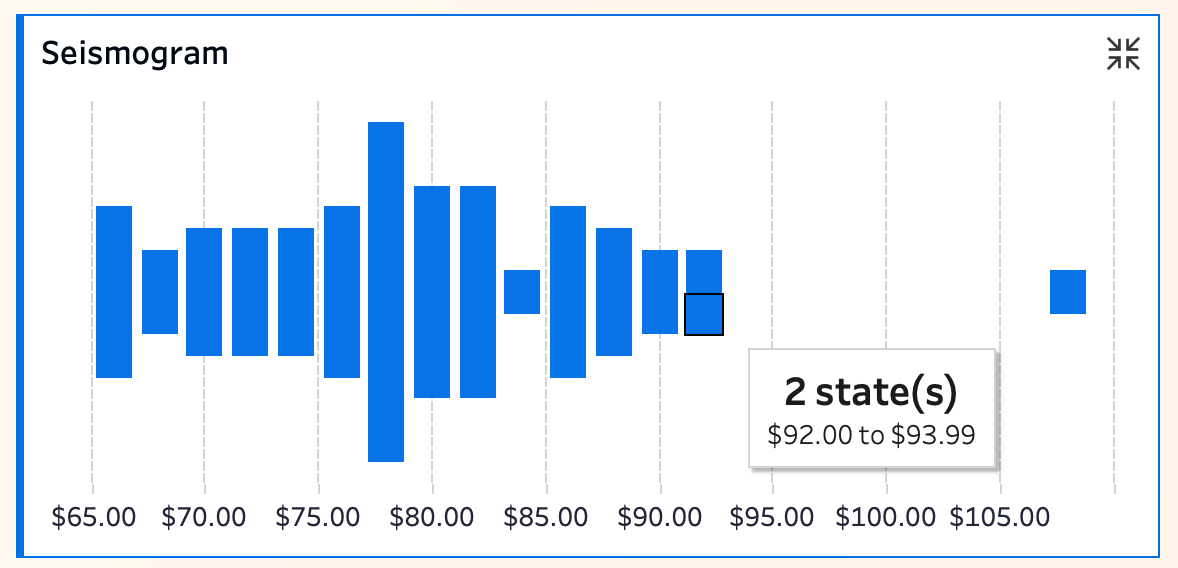
本质上，它继承了直方图的所有细节表达，但更突出数据的“波动感”和分布高低的层次感。

👉 和直方图相比，震波图更直观地表达了分布的整体走势和局部变化，尤其适合发现主峰、次峰以及整体是否对称等信息，适合样本量较大、分布不规则的分析场景。正因如此，Kevin 给出了最高评分，认为它是全局与细节兼顾的最佳选择之一。

👉 不过，震波图同样受限于数据桶宽度的设置，合适的分组能够呈现清晰分布，否则可能掩盖细节或造成误导。而且，初次接触的用户可能需要适应其“镜像结构”的表达方式。

08 圆角震波图

圆角震波图（Rounded Seismogram）是震波图的美观进阶版，通过将柱状替换为圆角形状，整体视觉效果更为柔和和现代。

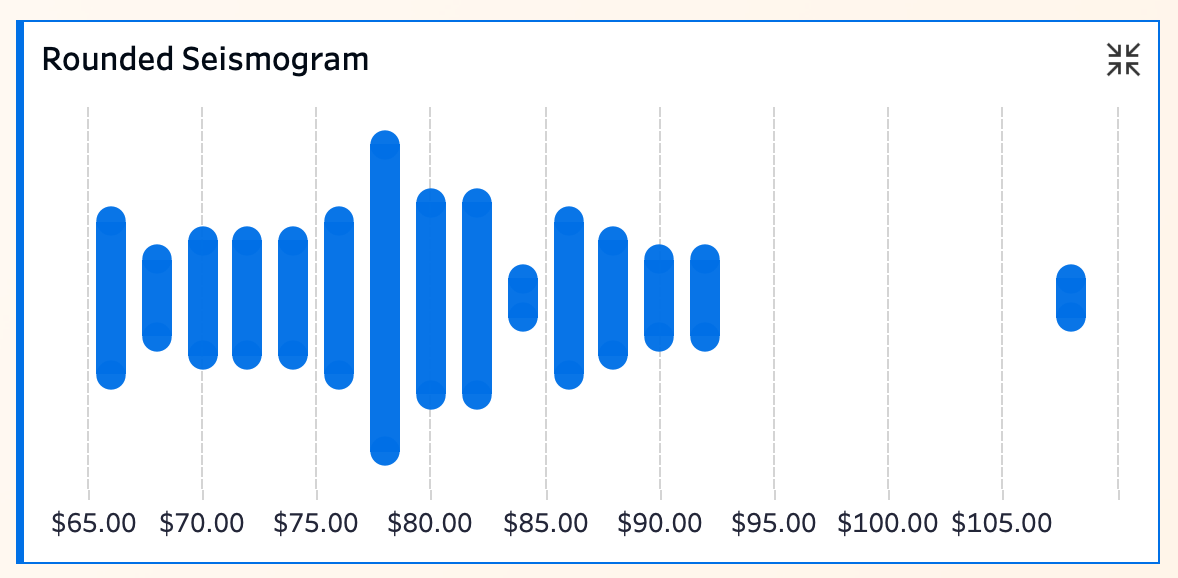
👉 在表达数据分布特征上，它依然具备震波图突出的优势：可以非常直观地展现分布的主峰、低谷以及异常值，尤其适合大数据量、不规则分布的数据分析场景。

👉 不过，这种圆角设计并没有带来本质上的信息增量。它和直方图一样，依然受限于数据桶宽度的设置。同时，圆角元素需要更多的设计和调整，在数据量很大时，柱形和圆角的大小、间距等因素都可能影响最终的可读性和美观度。

09 分组蜂群图

分组蜂群图（Binned Beeswarm Plot）是在直方图的基础上引入圆形符号，每个圆点代表一个数据观测值，并在每个价格区间内按垂直方向“堆叠”展示。

当某个价格区间的圆点越多、竖向高度越高，就说明该区间的数据点越密集。这样，既能看到每个区间内具体有多少州落在某一价格段，又能直观感受到分布的主峰、低谷和异常点。

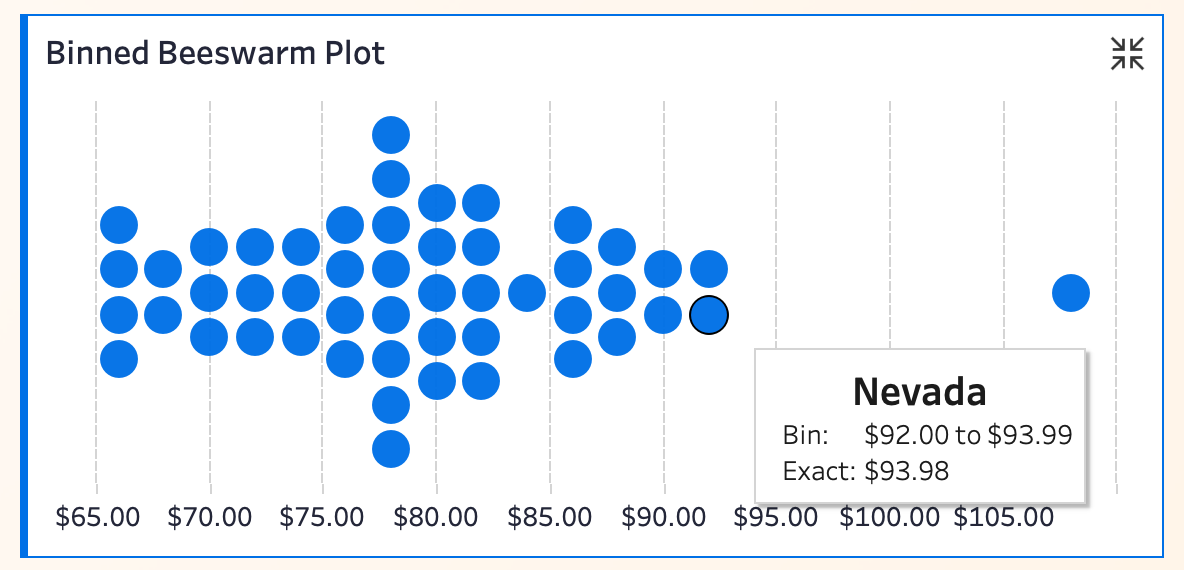
👉 相比传统直方图，分组蜂群图在样本量较小时优势突出：你可以直接“数圆点”，判断每个价格区间的真实分布，无需估算条形高度。此外，圆形的排列让整体视觉更加友好，分布结构一目了然。所以，Kevin 认为它非常适合用于小样本分布、讲究数据颗粒度的分析和展示场景。

👉 局限性方面，分组蜂群图的可读性依然会受到数据桶宽度影响，如果分组不合理，分布结构依然可能被掩盖。同时，当样本量很大时，圆点会大量重叠或挤压，反而影响阅读体验。

10 方格单元直方图

通过把传统直方图“拆解”为一个个小方块，每个方块就代表一个数据观测值。这样，就不再只是“估算”条形高度，而是支持直接数出每个价格区间到底有多少个州分布其中。

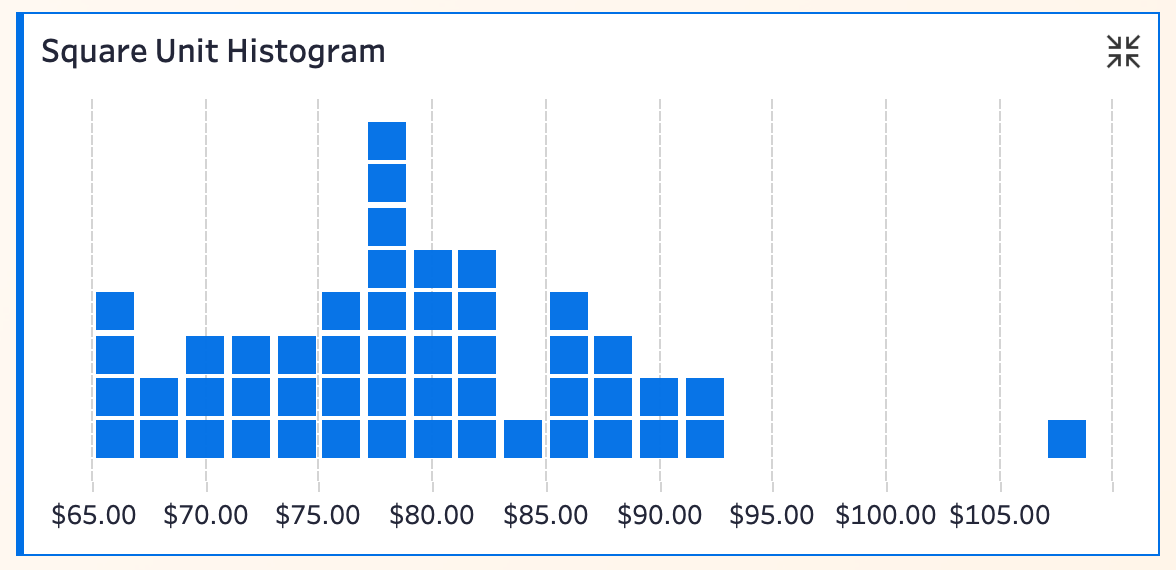
👉 对于小样本数据来说，方格单元直方图（Square Unit Histogram）让分布结构更加具体且颗粒度更细，特别适合数据量不大、需要精确呈现每个观测值时使用。

👉 不过，方格化的设计也带来了新的可视化挑战。当样本量变多或价格区间划分不合适时，方格间距和排列容易造成“网格错觉”，影响整体美感和可读性。整体分布形态仍受数据桶设置影响，分组策略不佳会让分布解读变得困难。此外，在大样本场景下难以兼顾效率和清晰度。

正因如此，Kevin 只给出了中等的三星评分，认为它适合用在对数据量级不大、需要让报表用户“看到每一个点”的呈现场景，但美观与效率之间需要权衡。

11 圆点单元直方图

在可视化分析中，圆点单元直方图（Circular Unit Histogram）常被用来强调“每一个数据都不可忽视”。它将每个观测值以圆点堆叠的方式展现出来，既保持了分布结构的直观性，又让整体视觉更加柔和。

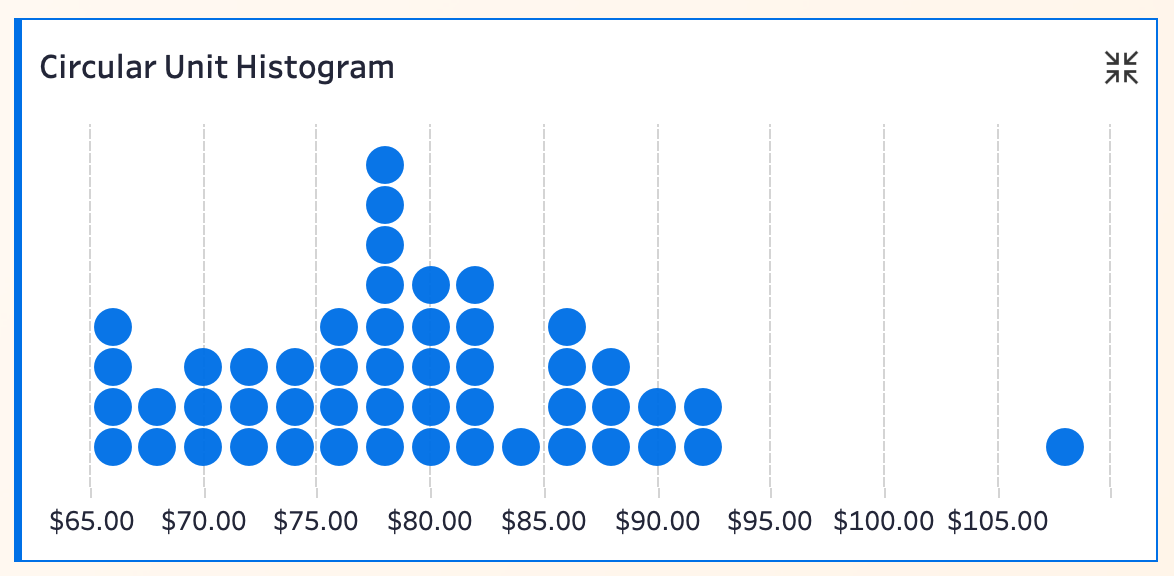
尤其在样本量不大的情况下，用户可轻松查看每个价格区间里究竟有多少州。主力区间点多且密集，异常值则显得尤为突出，整体分布一目了然。

👉 此外，相比用方格来表达，圆形符号更容易让人接受，也能有效避免网格化排列带来的生硬感。尤其在面向非技术用户或注重美观的业务汇报时，是个不小的加分项。

👉 当然了，这种方式依旧需注意分组（数据桶）的设置，分组过宽或过窄都可能影响分布解读。数据量较大时，圆点也会出现堆叠、遮挡的问题，不过在小样本场景下依然非常实用。

总的来说，圆点单元直方图在细节展现和视觉美感之间取得了较好的平衡。这也解释了为什么 Kevin 会给出较高的 4 星评价，它确实在实际工作中用得上。

12 蜂群图

蜂群图（Beeswarm Plot）算是一种非常极致的分布可视化方式了。如下图，每个圆点精确对应一个州的价格，圆点的横坐标就是真实的价格数值，竖直方向则是为了避免重叠而人为调整，使其都能被“看到”。

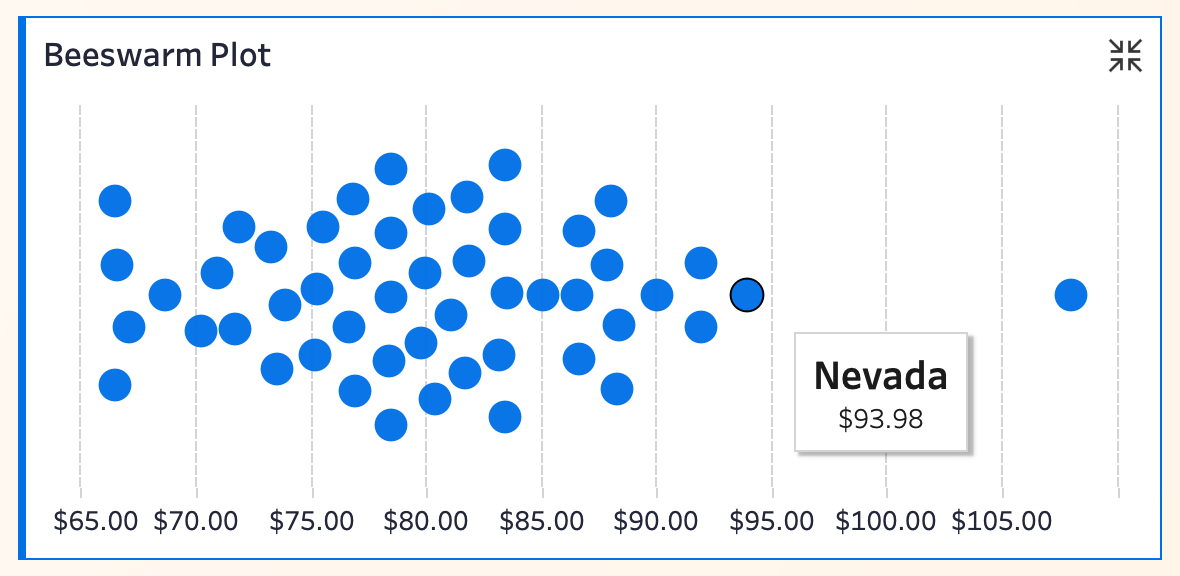
👉 和直方图、分组蜂群图等方案相比，蜂群图的优势在于精细度和个体可读性。你可以准确感受到整个分布的结构，同时也能直接定位某个具体观测点。

从适用场景看，蜂群图尤其适合数据量不是很大的时候。数据一旦太多，圆点还是会挤成一片。另外，对于强调展示美观和每个数据都值得被关注的汇报，它是不错的选择。

👉 不过，这种图表实现起来有点门槛：目前用 Tableau 原生功能实操起来比较复杂，需用额外的扩展程序或脚本生成，这对普通用户来说不太友好。因此，Kevin 虽然认可蜂群图的表达力，但实际应用给了 3 星的评价，更多是因为制作门槛，而不是因为表达力不足。

如需实现类似效果，可以参考：举个栗子！Tableau 技巧：用可视化项扩展程序，快速实现蜂群图 Bees warm Plot。

数据分布可视化最佳实践

最后，我们总结一下应该如何选择合适的分布可视化图表。最佳实践规则是：选用图表时应结合数据特性、分析目标和报表用户的数据素养，让数据分布的“真相”更容易被看见！

• 箱线图（盒须图）适合展示总体分布与对比，但不宜单独使用。

• 直方图/震波图/单位图可还原分布细节，推荐用于初步探索和说明趋势。

• 蜂群图/分组蜂群图/抖动点让每个原始数据点都“看得见”，适合分析局部密集区、异常值和个体特征，尤其适合数据点较少的情况。

如有需要，可点击访问 Tableau Public，进一步探索 Kevin 分享的工作簿。